《神经网络与深度学习》第7章
高维变量的非凸优化
之前我们遇到的问题都是使用梯度下降法会陷入局部最优点无法逃离,事实上这只是在低维空间中,现在的多数机器学习任务都是在高维空间中的,并且遇到的大多数都是鞍点,因此,非凸优化的难点并不在于如何逃离局部最优点,而是如何逃离鞍点,如图所示:

从数学上解释鞍点很简单,鞍点的特征是一阶梯度为0,但 是二阶梯度的 Hessian 矩阵不是半正定矩阵,如图,在二维空间中,这只是一条曲线,显然这个时候已经到达了最低点,而在三维空间中这显然没有到达最低点。
对比于局部最优点来说,鞍点并不可怕,相反,我们更希望的是遇到鞍点。如何逃离鞍点呢?现在我们将损失函数$L(\theta)$泰勒展开:
$$
L(\theta)\approx L(\theta’)+(\theta-\theta’)^Tg+\frac{1}{2}(\theta-\theta’)^TH(\theta-\theta’)
$$
如果我们今天走到的是局部最优点,那么梯度g=0,于是上述公式便可以化简为:
$$
L(\theta)\approx L(\theta’)+\frac{1}{2}(\theta-\theta’)^TH(\theta-\theta’)
$$
我们记$(\theta-\theta’)$为$\pmb{v}$,$H$为 Hessian 矩阵.
对于所有的$\pmb{v}$,现有三种情况:
- $\pmb{v}^TH\pmb{v}>0$,可以得到$L(\theta)>L(\theta’)$,那么就是局部最低点。等价于$H$是正定矩阵(特征值都是正的)。
- $\pmb{v}^TH\pmb{v}<0$,可以得到$L(\theta)<L(\theta’)$,那么就是局部最高点。等价于$H$是负定矩阵(特征值都是负的)。
- $\exists\pmb{v}^TH\pmb{v}>0,\exists\pmb{v}^TH\pmb{v}<0$,那么就是鞍点。(特征值有正有负)
对于局部最优点,g=0,我们无法获知下一步参数更新方向,而对于鞍点,$H$可以告知我们下一步走参数更新方向。
现在记$\mu$为H的特征向量,$\lambda$为H的特征值,并且$(\theta-\theta’)$代入的就是$\mu$,则有$\mu^TH\mu=\mu^T(\lambda\mu)=\lambda|\mu|^2$.
如果$\lambda<0$,那么$\lambda|\mu|^2<0$,于是有$L(\theta)<L(\theta’)$.
此时$\theta-\theta’=\mu\Rightarrow\theta=\theta’+\mu$,这时就可以减小L,也就是让$\theta$沿着特征值$\mu$的方向去更新,就可以降低损失。
为什么要批量训练?
如图所示,左边相当于没有使用批量训练,需要看过所有的训练资料再进行参数更新,右边每看过一个训练资料便进行参数更新。所以,哪个方法比较好呢?看起来左边的更新方向比较“稳”,而右边的更新方向较为“曲折”,并且左边更新一次参数的时间远远大于右边,但事实并不是这样。

由于并行运算的存在,比较大的batch size更新一次参数的时间并不一定比小的batch size更新一次参数的时间长,如下图所示,小的batch size和大的batch size每次更新参数花费的时间几乎差不多,除非size超过了并行运算的极限,时间才会倍数增加。由于这样的原因,小的batch size跑完一个epoch所花费的时间将远远大于使用大的batch size跑完一个epoch所花费的时间。

讨论到这里,我们发现使用大的batch size不仅参数更新方向更为稳定,并且花费的时间也较少,那么是否大的batch size比小的batch size好呢?事实反而相反,如下图所示:

这里可以看到,batch size越大,模型的准确性反而在降低,为什么?
如图,如果我们选择full batch,也就是不使用批量下降,那么如果我们的损失函数遇到局部最优点,那么很可能发生的情况就是模型无法训练下去,陷在了局部最优点上,而如果我们选择批量下降,那每个bacth的损失函数可能略有差异,于是即使在L1上陷入了局部最优点 ,也可以在L2上走出来。

《ON LARGE-BATCH TRAINING FOR DEEP LEARNING: GENERALIZATION GAP AND SHARP MINIMA》
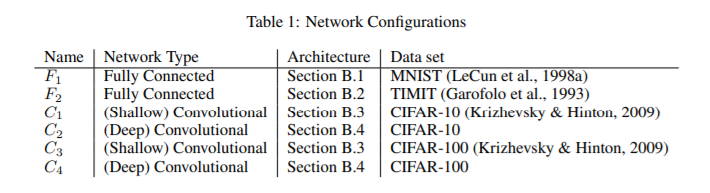
and_large-batch(LB)variants_of_ADAM_on_the_networks.png)
从上面两个表中可以得出:即使是将使用large batch和small batch的模型在训练集上的准确率训练得差不多,但是使用large batch和small batch的模型在测试集上的表现却不相同,很明显,使用small batch的模型在测试集上的表现更好。
why?如图,文中给出的解释是:

在训练集和测试集上LOSS函数的差异如图,Sharp Minimum在训练集和测试集上的表现会相差很大,而Flat Minimum在训练集和测试集上的表现不会相差很大,使用small batch size趋向于走向Flat Minimum,而使用large batch size趋向于走向Sharp Minimum。
当然batch size也是一个超参数,同样需要自己的调整,并且现在也有相关技术可以同时兼得large batch size训练快,small batch size训练表现好的优点,具体可以参考比如LARGE BATCH OPTIMIZATION FOR DEEP LEARNING: TRAINING BERT IN 76 MINUTES
《神经网络与深度学习》第7章