《智能计算系统》第六章
第六章 深度学习处理器原理
6.1 深度学习处理器概述
6.1.1 深度学习处理器的意义
随着神经网络算法的发展,神经网络从只有输入和输出层的感知机,发展到有一个隐层的多层感知机,再到深度神经网络。在这个过程中,伴随着神经网络的层数、神经元数量、突触数量的不断增长,传统芯片CPU、GPU已经难以满足神经网络不断增长的速度和能效需求。由此诞生了深度学习处理器。
6.1.2 深度学习处理器的发展历史
早期的神经网络计算机/芯片只能处理很小规模的浅层神经网络算法,未能取得工业实践中的广泛应用。随着深度学习技术的兴起,推动了人工智能芯片的研究和发展。
深度学习处理器的蓬勃发展主要得益于以下三个方面:
(1)深度学习应用广泛
(2)集成电路工艺发展放缓
(3)计算机体系结构技术的发展
6.1.3 设计思路
整个体系结构最重要的问题:算法范围界定和算法分析。深度学习处理器需要在通用性和灵活性之间取得平衡,既要能效高,又要能对深度学习应用有全面的支持。深度学习处理器需要具备可编程的能力,通过编程来支持深度学习编程框架中已有的深度学习算子,甚至是未来的算子。
因此,设计深度学习处理器时,首先要分析算法的计算特性和访存特性,然后根据算法特性,确定深度学习处理器的微体系结构,包括指令集、流水线、运算部件、访存部件。
6.2 目标算法分析
以本书驱动范例,针对VGG19进行分析。
6.2.1 计算特征
不同层的计算特点如表所示:
| 层 | 计算类型 | 乘加操作个数 | 激活函数操作个数 |
|---|---|---|---|
| 卷积层 | 矩阵内积、向量的元素操作 | $N_{if}\times N_{of}\times N_{or}\times N_{oc}\times K_{r}\times K_{c}$个乘加 | $N_{of}\times N_{or}\times N_{oc}$ |
| 池化层 | 向量的元素操作 | $N_{if}\times N_{or}\times N_{oc}\times K_{r}\times K_{c}$个加法或比较$+N_{if}\times N_{or}\times N_{oc}$个除法操作(平均池化) | 无 |
| 全连接层 | 矩阵乘向量,向量的元素操作 | $N_{o}\times N_{i}$个乘加 | $N_{o}$ |
6.2.2 访存特征
不同层的重用特点如表所示:
| 层 | 可重用 | 不可重用 |
|---|---|---|
| 卷积层 | 输入神经元、输出神经元、突触权重 | 无 |
| 池化层 | 当池化窗口大于步长时,部分输入神经元可重用 | 当池化窗口小于等于步长时,输入神经元、输出神经元都不可重用 |
| 全连接层 | 输入神经元、输出神经元 | 突触权重 |
6.3 深度学习处理器DLP结构
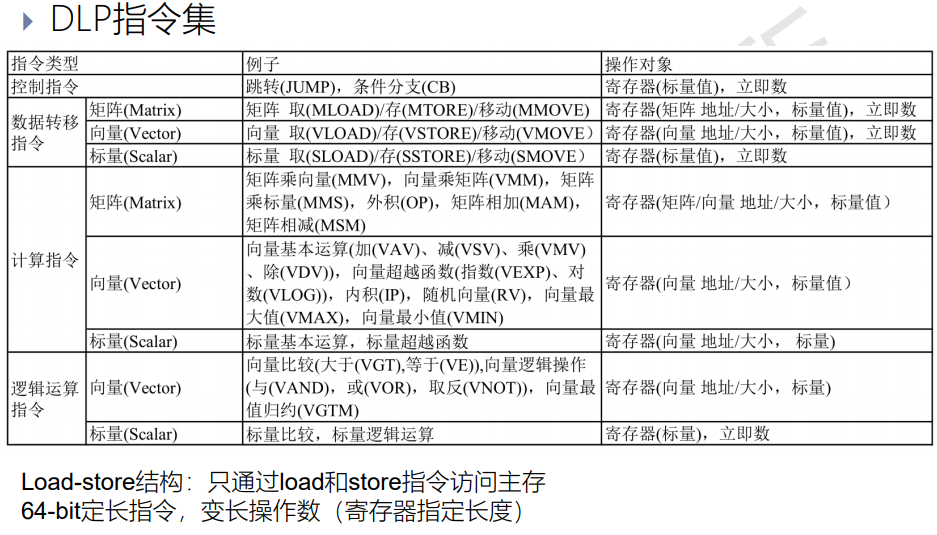
6.3.1 指令集
硬连线方案为每个神经网络提供专门的硬件控制逻辑,这种方案对特定神经网络能效极高,但无法支持新的神经网络,通用性差。
指令集方案是把各种神经网络层或算子拆分成一些基本的操作,每个操作由一条指令来完成。只要指令集覆盖了各种深度学习算子的最大公约数,新的神经网络层就能够由这些指令拼接组合起来,因此指令集方案兼顾了能效和通用性。
在提升并行性方面,采用数据级并行,数据级并行是指一条指令可以同时处理多个数据。数据级并行的优点在于指令数较少,因而指令流水线功耗、面积开销小。虽然指令级并行的灵活性高,但其指令流水线控制通路复杂,功耗和面积开销都很大,由于深度学习中主要是规整的向量、矩阵操作,并且迫切需要提升效率,降低功耗和面积开销,所以采用数据级并行的指令集。
6.3.2 流水线
DLP的一条指令执行主要经历7个流水线阶段:取指、译码、发射、读寄存器、执行、写回、提交。DLP深度学习处理器架构如图所示:
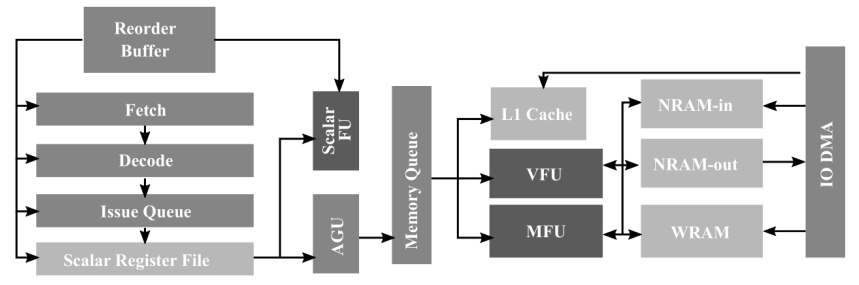
其中,VFU为向量功能单元,MFU为矩阵功能单元。
6.3.3 运算部件
6.3.3.1 向量MAC
下图是一个最基本的标量MAC单元,功能是完成一个乘加操作,它的输入是两个标量a和b,它的输出为两个标量的乘积加上原始值c,即$a\times b+c$。

而向量MAC的输入则是两个向量$a=[a_1;a_2;a_3;\cdots;a_N]$和$b=[b_1;b_2;b_3;\cdots;b_N]$,输出为两个向量的内积再加上原始值c,即
$$
\sum_{i=1}^Na_i\times b_i+c
$$
输入为两个N维向量的MAC,每个时钟周期可以完成一个N输入1输出的神经网络全连接层的计算。如果DLP集成了M个向量MAC,那么每个时钟周期就可以处理完成一个N输入M输出的神经网络全连接层的计算。
6.3.3.2 对向量MAC单元的扩展
对向量MAC单元作如下改进,以支持VGG19网络中前向计算的所有算子。
(1)增加可重构的非线性激活函数的运算部件。
(2)增加局部累加器,支持加偏置的运算。
(3)增加MFU-1/MFU-2/MFU-3的退出通路以支持池化运算。

6.3.3.3 MFU和VFU
MFU和VFU分别用于支持矩阵指令和向量指令,因此MFU支持矩阵向量乘指令MMV、向量矩阵乘指令VMM、矩阵标量乘指令NMS、外积乘指令OP、矩阵加矩阵指令MAM和矩阵减矩阵指令MSM。而VFU则需要支持神经网络算法中单纯的一维向量操作指令,而无需实现在MFU上,降低MFU的复杂度,提高向量操作的灵活性。
6.3.4 访存部件
深度学习处理器采用Scratchpad Memory管理方案,将输入神经元、输出神经元、突出权重这三类数据放在不同的片上存储器上(可解耦性),形成“运算单元-片上-片外“的存储架构,提高片上数据复用率。分别为NRAM-in(输入神经元缓存)、NRAM-out(输出神经元缓存)和WRAM(权重缓存)。
6.3.5 算法到芯片的映射
由于输入神经元/输出数据元的个数数量级非常高,现阶段没有任何单个芯片足以放下100万个乘法器,因此在计算过程中硬件运算必须时分复用。在每个计算周期只用一小块的输入数据去计算一小块的输出数据,下一计算周期计算下一小块的输出数据,最后汇总得到最终的输出数据。
6.4 优化设计
6.4.1 基于标量MAC的运算部件
由于卷积运算中存在多种数据可复用性,在设计标量MAC的运算单元时可以有效地利用这些特性,其一种实现如图所示:

通过PE间的数据传递来获得所需要的数据,可以有效地减少片外访存带宽,缓解访存压力。
6.4.2 稀疏化
采用稀疏化的方法,可以大幅降低神经网络的计算量和数据量。我们可以对权重稀疏化,也可以对神经元稀疏化,也可以动态稀疏化。利用稀疏的基本思路有两个,一个时是只计算非稀疏的部分,一个是直接跳过稀疏部分。前一种思路需要在计算前先对稀疏数据做处理,把里面的零去掉,从而把稀疏数据变成稠密数据,最后通过硬件单元直接计算,这样所得的计算结果都是有效数据。这种思路可以高效地利用稀疏,不仅可以加快计算速速,还可以高能效,但是需要对硬件做较大的改动。而后一种思路,硬件改动简单,只需要判断输入是否为零,如果为零,则输出直接为零。
为了进一步利用神经网络稀疏化的特点来降低存储和访存带宽,可以把稀疏化和量化压缩结合起来,最后神经元和权重所需的片上存储空间和访存带宽可以减少到十分之一左右。
6.4.3 低位宽
在处理器设计时采用更低位宽的运算器,虽然很多神经网络算法在计算时采用32位的单精度浮点数,但实际上16位定点数或者8位定点数已经足够满足应用需求。
6.5 性能评价
6.5.1 性能指标
深度学习处理器衡量计算能力的常用指标是TOPS(Tera Operations Per Second),即每秒执行多少万亿次操作。
$$
TOPS=f_c\times (N_{mul}+N_{add})/1000
$$
处理器主频 $f_c$的单位是 GHz,$N_{mul}$ 和 $N_{add}$分别表示每个时钟周期执行多少乘法或加法操作。
处理器的实际性能还受到访存带宽BW的影响,包括访问外存的带宽、访问多级片上存储的带宽。其中
$$
BW=f_m\times b\times \eta
$$
表示访存带宽BW与存储器的主频$f_m$ 、存储位宽 $b$、访存效率 $\eta$的关系。
6.5.2 基准测试
基准测试程序MLPerf:

6.5.3 影响性能的因素
一个深度学习任务的运行时间可以写为:
$$
T=\sum_iN_i\times C_i/f_c
$$
其中𝑁𝑖表示该任务中第i类操作的数量,𝐶𝑖表示完成第i类操作所需要的时钟周期数,𝑓𝑐表示处理器的主频。
因此,为了减少深度学习任务的处理时间,可以从以下几个方面入手:
首先,减少经常出现的操作的执行周期数;其次,利用数据局部性,减少访存开销;最后,多级并行。
6.6 其他加速器
如表所示,DLP和其他加速器的比较:
| 类别 | 目标 | 速度 | 能效 | 灵活性 |
|---|---|---|---|---|
| DLP | 深度学习专用 | 高 | 高 | 深度学习领域通用 |
| FPGA | 通用可编程电路 | 低 | 中 | 通用 |
| GPU | SIMT架构矩阵加速 | 中 | 低 | 矩阵类应用通用 |