2021-12-03发表CS21717 分钟读完 (大约2540个字)0次访问

Roofline and TPU Performance

任何模型都必须依赖具体的计算平台才能展示出自己真正的实力。从前，许多的性能模型和模拟器都是通过追踪延迟来预测性能，近二十年也诞生了一些隐藏延迟的技术，例如：乱序执行（硬件发现并行性以隐藏延迟）；硬件流预取（硬件推测加载数据）；大规模线程并行。这些技术有效地隐藏了延迟，但同时也使得计算平台从延迟受限转变为了吞吐量受限。

Roofline模型是一个吞吐量指向的性能模型，它追踪速度而不是时间。也可以这么说说Roof-line Model就是：模型在一个计算平台的限制下，到底能达到多快的浮点计算速度。通俗来讲是”计算量为A且访存量为B的模型在算力为C且带宽为D的计算平台所能达到的理论性能上限E是多少“这个问题。Roofline模型有两个关键部分：一个是机器参数，第二个是应用的理论编辑。

首先介绍计算平台的两个指标：算力$\pi$和带宽$\beta$

算力$\pi$：计算平台的性能上限，即一个计算平台每秒钟所能完成的浮点运算数的极限。单位是 FLOP/s。
带宽$\beta$：计算平台的带宽上限，即一个计算平台每秒钟所能完成的内存交换量的极限。单位是 Byte/s。
计算强度上限$I_{max}$：即单位内存交换最多可进行多少次浮点预算，单位为 FLOPs/Byte。
$$
I{max}=\frac{\pi}{\beta}
$$
其次介绍模型的两个指标：计算量与访存量
计算量：指的是输入单个样本，模型进行一次完整的前向传播需要的浮点运算数，也即模型的时间复杂度。单位是 FLOPs。
访存量：指的是输入单个样本，模型完成一次前向传播过程中所产生的内存交换总量，也即模型的空间复杂度。在理想情况下（即不考虑片上缓存），模型的访存量就是模型各层权重参数的内存占用（Kernel Mem）与每层所输出的特征图的内存占用（Output Mem）之和。单位是Byte。
模型的计算强度$I$：计算量除以访存量即模型的计算强度，它表示此模型在计算过程中，每Byte内存交换用于进行多少次浮点运算。单位是FLOPs/Byte。易知模型的计算强度越大，其内存使用效率越高。
模型的理论性能 $P$：即模型在计算平台上所能达到的每秒浮点运算次数（理论值）。单位是 FLOPS 。

Roofline模型在DRAM上如下图所示：

机器算力决定“屋顶”的高度，峰值性能。
访存带宽决定“房檐”的斜率，DRAM的访问速度。
x轴表示计算强度，y轴表示可达到的计算性能。
绿色虚线和紫色实线包裹的三角形区域是应用是带宽受限的，如图所示，Kernel 1：

当模型的计算强度$I$小于计算平台的计算强度上限$I_{max}$时，此时模型位于“房檐”区间，模型理论性能$P$完全由计算平台的访存带宽上限$\beta$（即“房檐”的斜率）以及模型自身的计算强度$I$决定，模型处于memory-bound状态。可见，在模型处于带宽瓶颈区间的前提下，计算平台的带宽$\beta$越大（房檐越陡），或者模型的计算强度$I$越大，模型的理论性能$P$呈线性增长。
绿色虚线右侧区域是应用是计算受限的，如图Kernel 2。

不管模型的计算强度$I$有多大，它的理论性能$P$最大只能达到计算平台的算力$\pi$。当模型的计算强度$I$大于计算平台的计算强度上限 $I_{max}$时，模型在当前计算平台处于compute-bound状态，即模型的理论性能$P$受到计算平台算力$\pi$的限制，无法与计算强度$I$成正比。但这意味着此时模型100%利用了计算平台的全部算力。可见，计算平台的算力$\pi$越高，模型进入计算受限区域后的理论性能$P$也就越大。

Roofline 根据内核的操作强度设置内核性能的上限。如果我们将操作强度看作是一根撞到屋顶的柱子，它要么撞到屋顶的平坦部分，这意味着性能受计算限制，要么撞到屋顶的倾斜部分，这意味着性能最终受内存限制。更多时候我们无法达到理论性能峰值，因为局部性（数据复用）和访存带宽会限制性能。

示例1：

一般机器的计算强度在5-10flops/byte的范围。图中示例程序需要读x[i]和y[i]，写z[i]，每次循环需要2个浮点操作，需要24个字节内存访问，则AI（Arithmetic Intensity，计算强度）=2/24=0.083，故处于访存受限。

示例2：

图中示例程序需要7次浮点操作，需要8次浮点访问（7次读，1次存），则AI=7/64=0.11，使用Cache可以将程序变为1次读1次写，故AI=7/16=0.44，故处于访存受限。

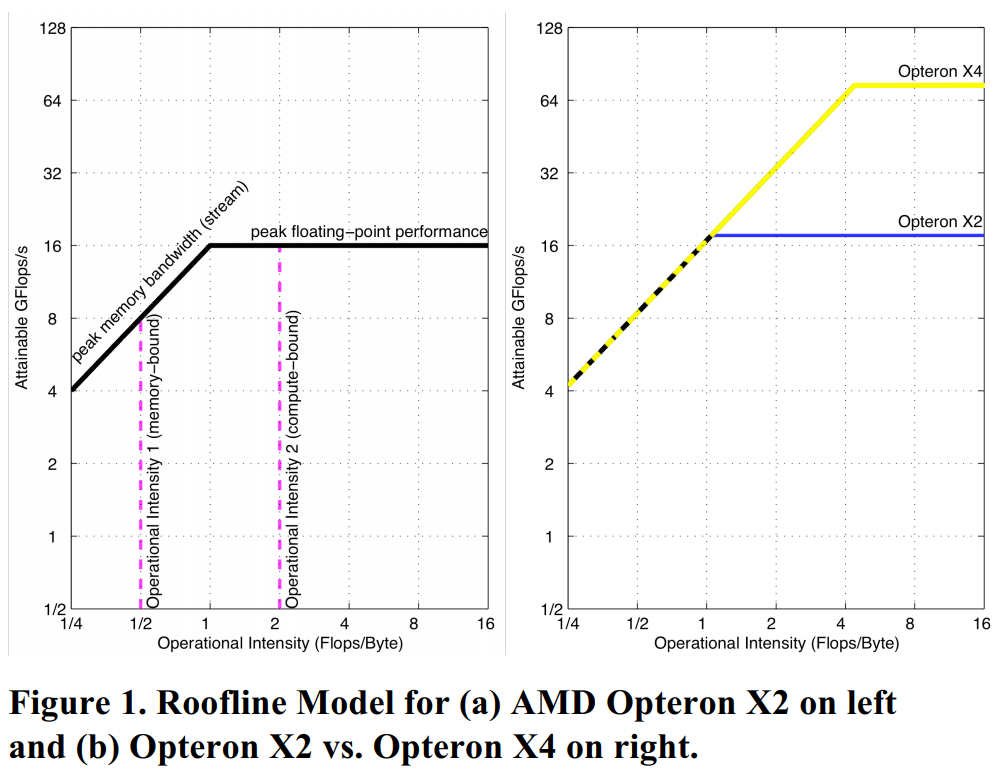
下图是不同产品Roofline模型的比较，图 1a 是具有两个内核的 Opteron X2的Roofline模型，将其与其后代产品Opteron X4进行比较，设定他们具有相同的内存系统，Opteron X4具有四个内核，并且X4的每个内核的峰值浮点性能也翻了一番，X4内核每个时钟周期可以发出两条浮点SSE2指令，而X2内核可以每隔一个时钟周期发出两条SSE2指令，由于X4时钟频率稍快，X2为2.2GHz，而X4为2.3GHz，所以X4 的峰值浮点性能是X2的四倍多，具有相同的内存带宽。如图1b所示，脊点从Opteron X2的1.0向右移动到了Opteron X4的4.4。因此，要在X4中获得基于X2的性能提升，内核需要有高于1的计算强度或者或者工作集能匹配X4的2M大小的L3Cache。

由于处理器一般都包含了多级存储：寄存器、L1,L2,L3级cache、HBM或者MCDRAM（设备内存）、DDR和NVRAM。所以应用在每一个层级都有局部性，每一个层级都有独立的带宽，每一层级的数据搬移都有独立的计算强度。因此如下图所示，图中叠加了L2、MCDRAM和DDR的Roofline模型，性能是受最小层约束的。